Unmanned Aerial Systems (UAS) Performance Optimization
In trajectory planning and control design for unmanned air vehicles, highly simplified models are typically used to represent the vehicle dynamics and the operating environment. To obtain more realistic and feasible trajectories, high-fidelity, six-degrees-of-freedom (6DoF) dynamic models of vehicles have to be considered. These high-fidelity models incorporate accurate aerodynamic and aero-mechanical models that will be used for all guidance (path-planning) purposes. Our research seeks to make use of advanced optimization algorithms to achieve the best operation of flying vehicles. In addition, the developed tools allow us to perform comprehensive analysis of the resulting optimal trajectories, which reveals major characteristics of each scenario. At the same time, closed-loop control systems are developed to follow the nominal trajectories in the presence of distrubances and uncertainties in model parameters and disturbance models. We are investigating multi-input, multi-output nonlinear model predictive controllers to enable enhanced tracking performance of optimal reference paths in near real time.


The wind model, aerodynamics, and control modules are integrated into a 6DoF flight simulation environment with a fully nonlinear flight controller (a back-stepping fully nonlinear control). Below are the time histories for a number of states that represent an ascent-cruise-descent profile in the presence of winds. Our goal is to perform develop rapid trajectory optimization methods and evaluate the performance of developed through flying quad-copters in our experimental platforms. A particular recent study of us shows that using simplified quadratic models for thrust and power of propellers may lead to significant differences for realistic analysis of wind-body interaction that takes places during the flight of quadcopters. This is an important result since the endurance and battery life of and their effective range of quadcopters is severely affected by power consumption. In addition, realistic integration of sub-systems of these flying vehicles leads to more accurate verification studies.

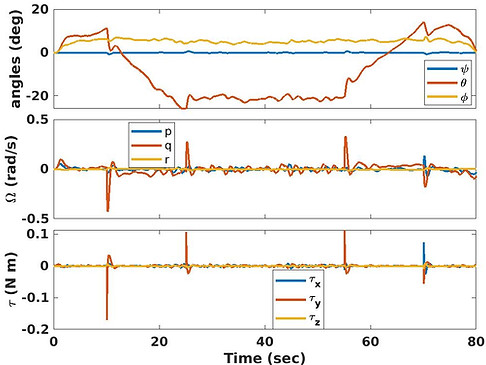
Aircraft/UAV Performance Optimization
To obtain more realistic and feasible trajectories, high-fidelity, 6DoF dynamic models of vehicles have to be considered. These high-fidelity models incorporate accurate aerodynamic and propulsion models that will be used for all path-planning scenarios. Our research seeks to make use of advance optimization algorithms (evolutionary algorithms such as particle swarm optimization (PSO), differential evolution (DE) and their hybrid with gradient-based methods) to achieve the best operation of flying vehicles. In addition, the developed tools allow us to perform comprehensive analysis of the resulting optimal trajectories, which reveals major characteristics of each scenario. At the same, a closed-loop control system has to be developed to follow the nominal trajectories. We are investigating advanced multi-input, multi-output nonlinear model predictive controller to enable the aircraft/UAV to track the optimal paths in near real time.
Aircraft Terrain Following/Avoidance
Terrain following/terrain avoidance (TF/TA) is of significant importance in many tactical (i.e., combat) and surveillance aircraft’s missions. In TF/TA, an aircraft maneuvers above and around the terrain to take advantage of the terrain masking to avoid radar detection. Control inputs could be the deflection angles of the aerodynamic surfaces (i.e., rudder, aileron, elevator) and the thrust magnitude and its orientation if the vehicle has thrust vectoring capability. The time history of these control inputs can be defined as decision variables and the task of optimization algorithm is to find the best combination of these decision variables such that a particular mission is performed while minimizing a prescribed performance index. These objectives could corresponds to time-, energy-, or height-optimal trajectories or a multi-objective optimization in which two or more objectives are taken into account.


Figure below depicts two minimum-time solutions for an aircraft that seeks to fly as close as possible to the terrain in order to avoid radar detection while avoids hitting the ground. The right plot shows the entire trajectory from a start point (in the lower left point) to a target point (on the upper right corner). The two left sub-plots depict height vs. time for the two best solutions that are obtained using particle swarm and differential evolution optimization methods. These global optimization algorithms have been fused with a sequential quadratic programming (SQP) optimization method to enhance the probability of finding the best solutions.

Figure below depicts two minimum-energy trajectories for an aircraft that seeks to fly as close as possible to the terrain in order to avoid radar detection while it avoids hitting the ground. A unique characteristic of minimum-energy trajectories is that the aircraft uses the terrain and positions itself in locations where its engine can be shut down and it can climb for a considerable portion of the flight.
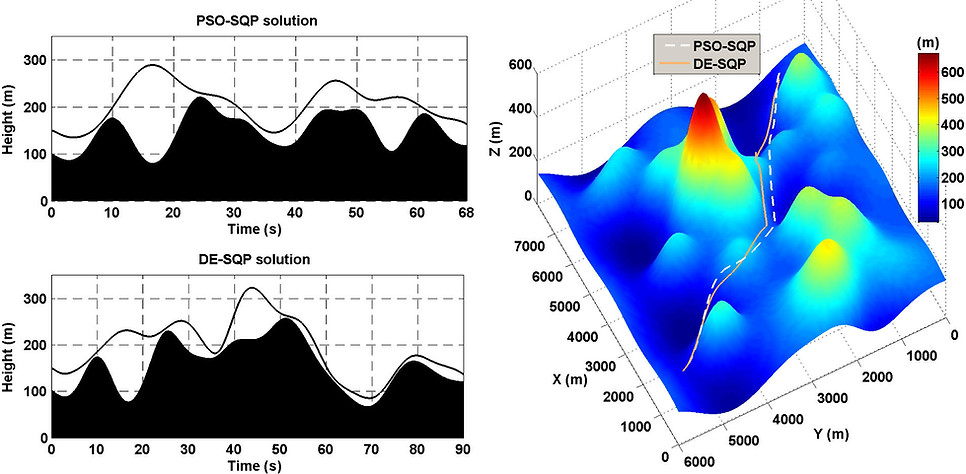
Figure below depicts two minimum-height trajectories for an aircraft that seeks to fly as close as possible to the terrain in order to avoid radar detection while it avoids hitting the ground. The right plot shows the entire trajectory from the lower left point to the upper right point. Compared to the above two cases, the aircraft follows the terrain more closely.

It is also possible to investigate the performance of the aircraft in reaching the target point in the presence of static or dynamic (with known dynamic behavior) radars that are viewed as threats to the aircraft. These radars are denoted by cones and are strategically placed over the terrain. Two of the radars are placed on the side of the main mountain of the terrain to analyze the performance. The aircraft still finds a suitable trajectory that avoids the targets and takes a different route that passes over the other side of the mountain.

Comparison of height-optimal trajectories also show the different paths taken with and without the presence of threats (i.e., radars).

It is also possible to consider a combination of fixed and moving threats (that have predictable motion). Figure below shows the top view of the same terrain while two of the threats have fixed locations, whereas the other two threats are moving toward each other. It is still possible for the aircraft to not only find a feasible trajectory, but also to find the lowest terrain to pass between the moving threats.

Selected Publications
-
Behdad Davoudi, Ehsan Taheri, et al., "Quad-rotor Flight Simulation in Realistic Atmospheric Conditions," AIAA Journal of Aircraft [under review], arXiv preprint arXiv:1902.01465
-
Berning, Andrew W., Ehsan Taheri., et al. "Rapid Uncertainty Propagation and Chance-Constrained Trajectory Optimization for Small Unmanned Aerial Vehicles." 2018 Annual American Control Conference (ACC). IEEE, 2018. https://ieeexplore.ieee.org/abstract/document/8431765/
-
Rastgoftar, Hossein, Ehsan Taheri., et al. "Continuum Deformation of a Multi-Quadcopter System in a Payload Delivery Mission." IFAC-PapersOnLine 50.1 (2017): 3455-3462. https://www.sciencedirect.com/science/article/pii/S2405896317313058
-
Kamyar, Reza and Ehsan Taheri. "Aircraft optimal terrain/threat-based trajectory planning and control." Journal of Guidance, Control, and Dynamics 37.2 (2014): 466-483. https://arc.aiaa.org/doi/abs/10.2514/1.61339
