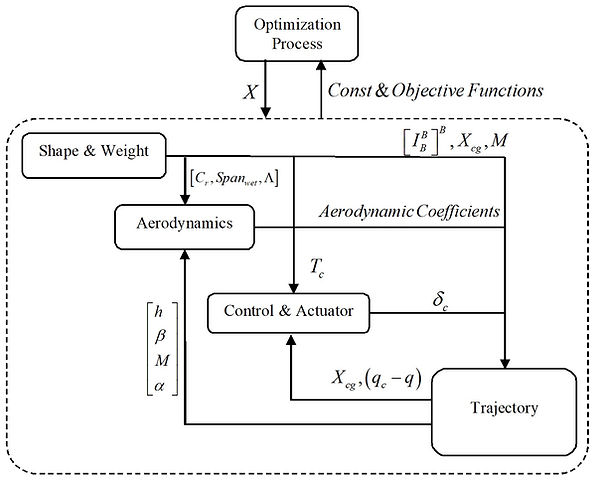
Multidisciplinary Design Optimization (MDO) is a branch of optimization that presents a distinct view when vehicle design is of interest. There are many disciplines of aerospace engineering that should collaborate to achieve the best vehicle performance. In a traditional approach to vehicle/system design, each discipline seeks to maximize certain parameters that measure performance. For instance, in aircraft design, the aerodynamics discipline seeks to design the most efficient aerodynamic configuration, whereas the structure discipline seeks to minimize the mass while considering acceptable safety margins. Similarly, the goal of the propulsion disciple is to size the best engine. Obviously, these disciplines have to collaborate with each other in order to converge to the best design. While not a very new concept, MDO presents a paradigm shift in design. It deviates from a discipline-centric design philosophy an offers a collaborative-based design approach that takes the interconnection of disciplines. The final design may not necessarily be ideal from the point of view of individual disciplines (i.e., not optimal from a local-discipline view), but the best performance is achieved.

 

Below is an example for an MDO approach to a two-stage launch vehicle design in which the size of the aerodynamic surfaces and vernier thrusters are optimized in order to achieve maximum payload that can be put into a parking orbit. For each set of parameters (stabilizer aerodynamic parameters and thrust value of four vernier thrusters), the weight and aerodynamic performance of the vehicles changes. The thrust of the vernier thrusters changes the mass and the aerodynamic parameters also change the mass of the vehicle. In addition, the aerodynamic performance of the vehicle changes. Therefore, it is important to update static and stability aerodynamic coefficients, which will be used for calculating aerodynamic forces and moments along a to-be-determined trajectory. A 6DoF flight simulation has been developed that has several components. One of the components performs 4-dimensional interpolations (over the altitude, Mach number, side-slip angle and angle of attack). A flight controller is also developed to track the optimal trajectory and determines the maximum deflection angles of the vernier thrusters that are responsible for attitude control of the vehicle. An (evolutionary) optimizer iterates over the feasible set of design variables and the objective value is returned. Eventually, the optimizer converges to the best configuration and set of parameters with respect to the defined constraints and objective function.