The above figure is a three-dimensional view of an optimal switching surface for a trajectory from Earth to asteroid Dionysus. The value of the so-called switching function, S, is given on the z axis. The other two axes represent time of flight and the value of thrust produced by the onboard engine. This switching surface represent an extremal field map of many neighboring optimal control trajectories. The condition of S = 0 is denoted by a plane colored in light blue. When indirect formalism of optimal control is used for trajectory optimization, the switching function, S, encodes the information as to when a spacecraft should switch its engine "on" or "off". If the value of switching function is positive, the optimality criteria demand that the engine has to be switched on and vice versa. So, those parts of the surface that are above the S = 0 plane correspond to regions in space when the engine has to be on. In the low-thrust region (that is, in the mountainous part of this plot), there is a dark blue color line. The entire line is above the plane except for a very short segment where it touches the plane. This means that for this particular thrust value, the engine has to operate during the entire time of flight.

 

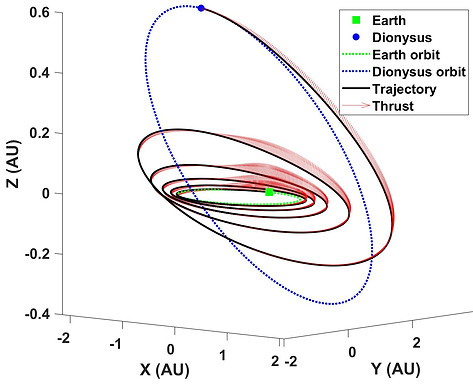
As the thrust value is increased (note that we are using logarithmic values for better visibility), the segments during which the engine has to operate shrink in time (of course, there are some exceptions). Therefore, we can initiate a procedure to start from the lowest feasible thrust (we coined it the minimum-thrust trajectory) and sweep the thrust value to very high values. The location, number and times of these small thrust segments at the very high thrust value correspond to an impulsive solution. The left figure below shows the trajectory that corresponds to the minimum-thrust trajectory (the dark blue line on the switching surface). It is obvious that the engine is entirely on during the trajectory (denoted by red arrows that exist during the entire trajectory). The right plot shows the limiting thrust value (impulsive) solution where the impulses are located at particular positions. There is also a large impulse at the intersection of the last ellipse and the orbit of the target body. This turns out to be the location at which the spacecraft is far from the Sun and it is ideal to perform plane-change maneuvers according to orbital mechanics principles.